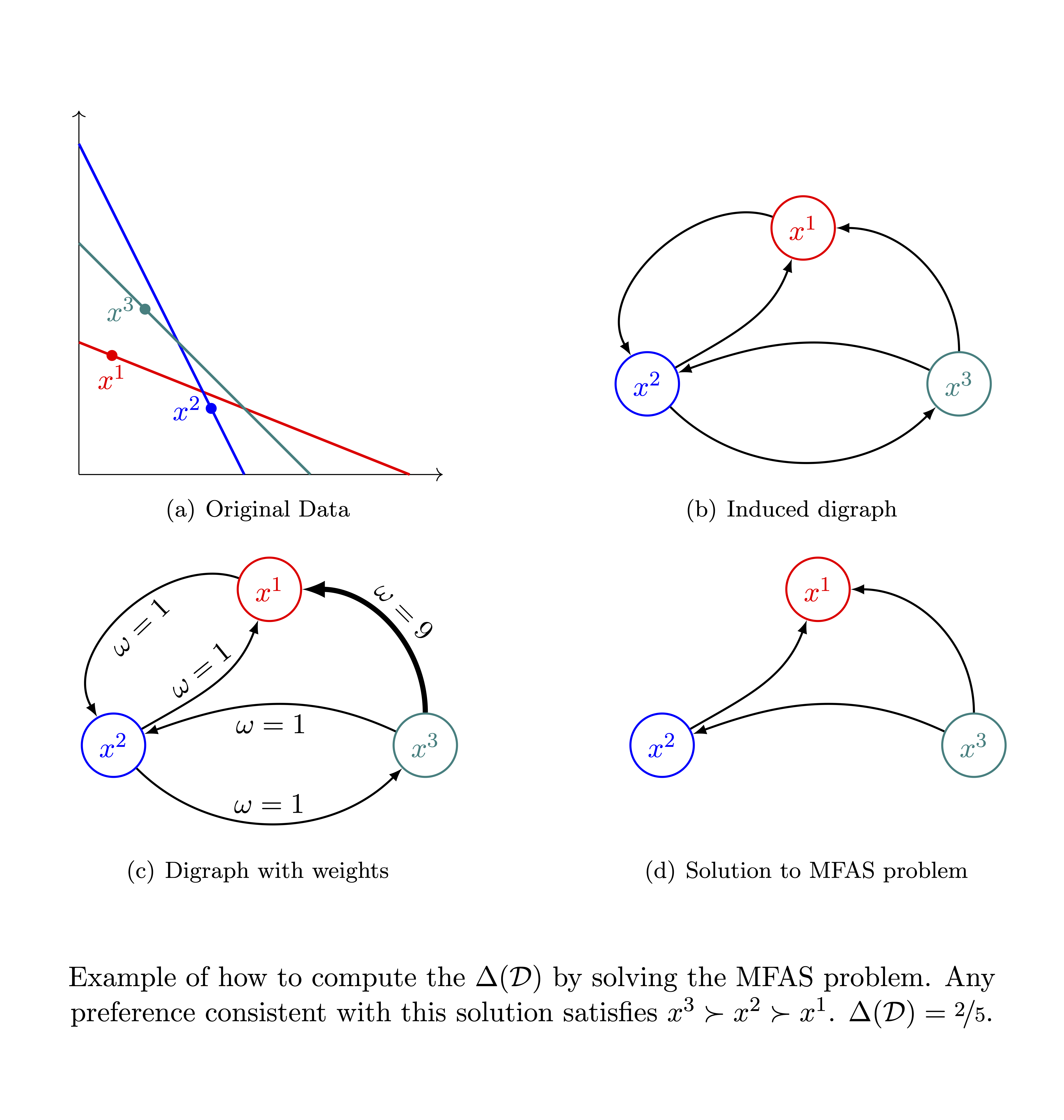
Preference Recoverability from Inconsistent Choices

We study the analysis of choices imperfectly aligned with the preference relation that drives them. First, we develop a measure of decision-making quality that, unlike the existing ones, ensures to asymptotically measure the distance between the subject's choices and her underlying preference (instead of some preference). We then use such a measure to propose a statistically consistent preference estimator. Empirical results suggest consistency is a relevant property when recovering preferences, especially for complex choice environments, compared to estimators based on intuitive motivations.

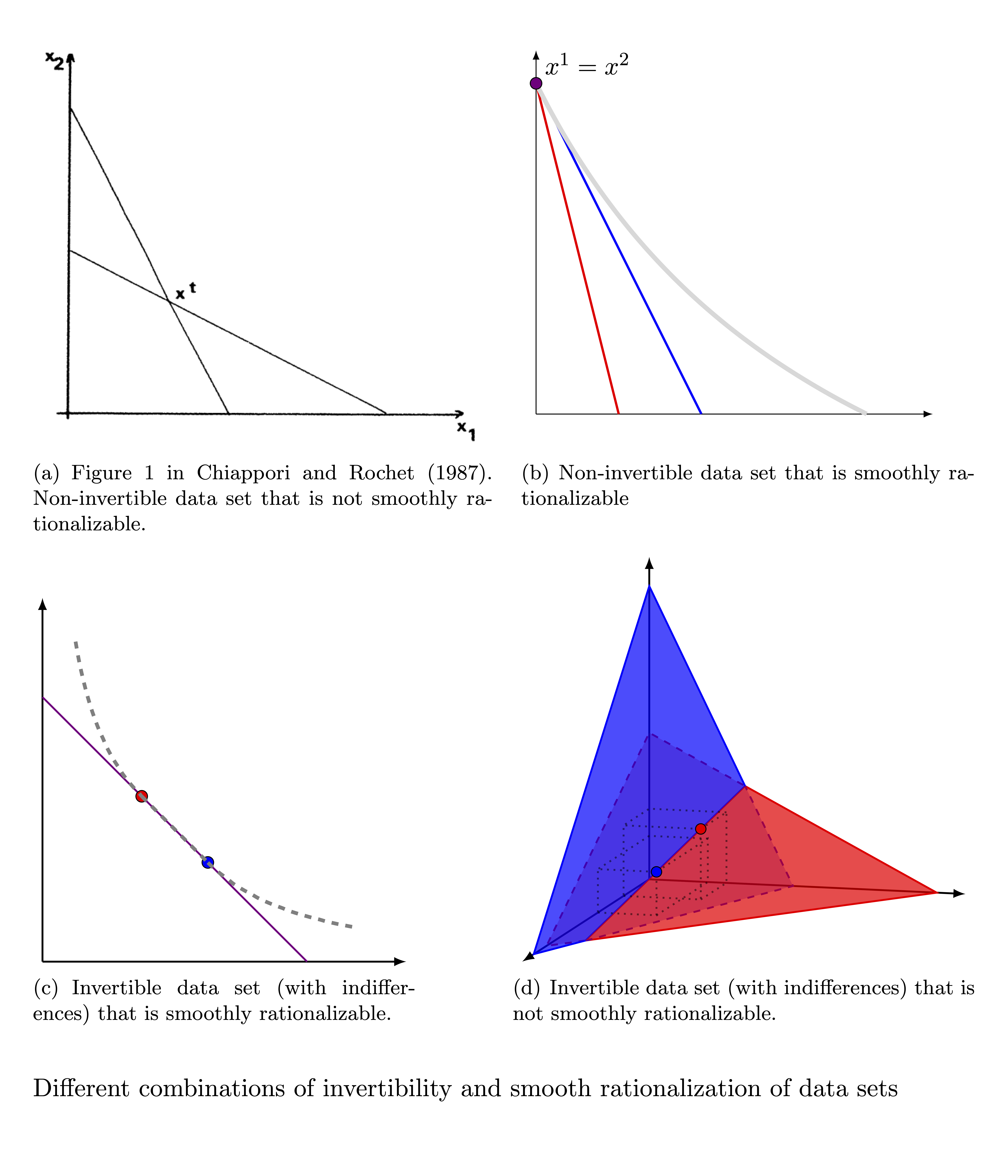
Smooth Rationalization

Economic models usually endow agents with (well-behaved) differentiable utilities. However, the behavioral implications of such an assumption are unclear. We study conditions under which choices can be rationalized by a differentiable utility, i.e., smoothly rationalized. Differentiability implies that indifferent choices have the same marginal rate of substitution. Starting from this observation, we develop an exact test for smooth rationalization. We also show that the existence of higher-order derivatives, commonly used for comparative statics, is empirically costless. We test smooth rationalization into several experimental data sets and find that, in most cases, choices are consistent with a differentiable utility.

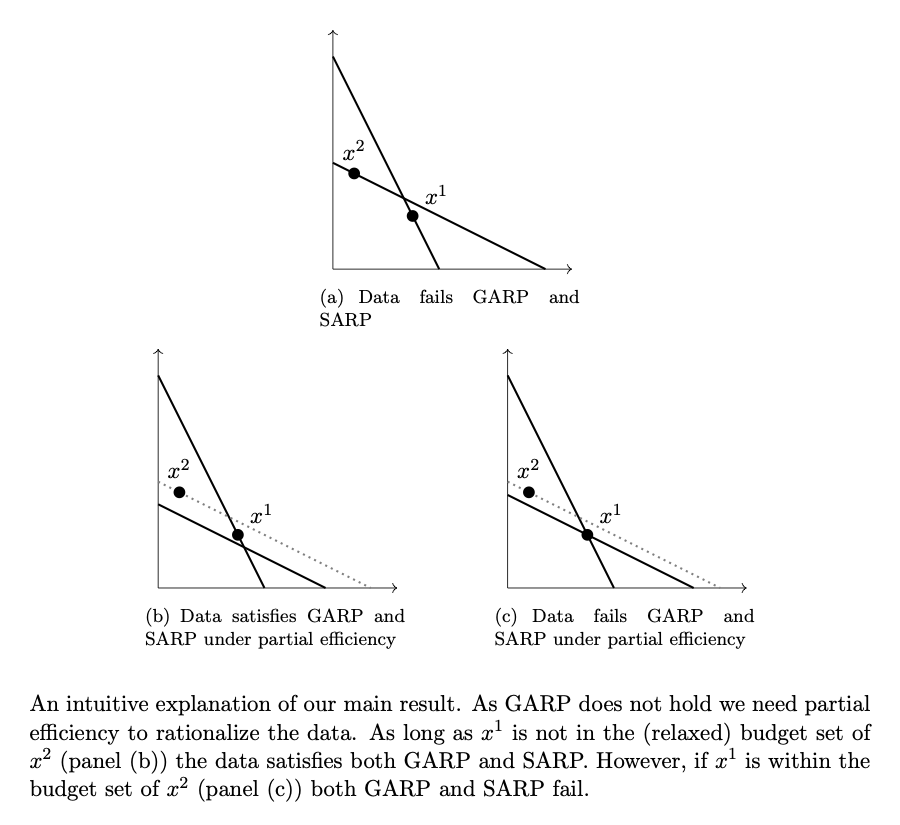
The generality of the Strong Axiom

Accepted at Economic Theory

Economic research usually endows consumers with a strictly concave utility function. When choices are rationalizable, this assumption can be tested by the Strong Axiom of Revealed Preferences, SARP, as if they fail such a test, the convexity of the utility is not strict. We extend this test to non-rationalizable choices using partial efficiency, the most popular method to recover preferences. Under partial efficiency, a strictly convex utility cannot be tested. Hence, the existence of a strictly concave utility is falsified if, and only if, choices are rationalizable but fail SARP, which we do not observe in laboratory data. From an empirical standpoint, our results suggest that assuming a strictly concave utility does not carry a cost.

Mathematical Finance, Information Flow, and Economic Growth in pre-industrial Europe

Old (and dormant) work for the Econ History class at UC Berkeley. Not as polished, but still a pretty cool result.

This paper studies the role of financial techniques development in Europe's economic growth from the thirteenth to the seventeenth century. During this era, mathematicians developed the main advances in finance, and Fibonacci’s book Liber Abaci is undoubtedly the most important development. This paper uses the publications of mathematics books as a measure of exposure to new financial techniques, and exploits city-level data. Results suggest that the of exposure to new financial technologies had a causal effect in economic growth before the sixteenth century. The presence of reverse causality and measurement error after the invention of the printing press make the effect impossible to identify after the sixteenth century.